三角函数公式

一、引言

在初中数学与高中数学的学习进程中，三角函数是一个极为重要的板块，它广泛运用于物理学、工程学、天文学等多个领域。无论是描述物体的周期性运动、分析电磁波的特性，还是计算天体的运行轨迹，都离不开三角函数的支持。而熟练掌握三角函数公式，则是运用这一强大数学工具的基础和关键。这些公式犹如构建知识大厦的基石，帮助我们深入理解和解决各种与角度、弧度相关的问题。

二、基本三角函数定义

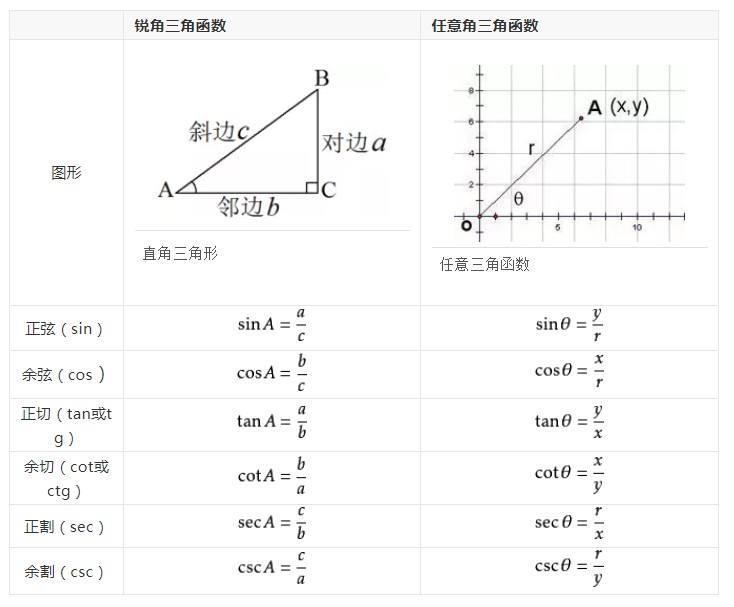
设角$\alpha$终边上一点$P(x,y)$，点$P$到原点的距离为$r = \sqrt{x^{2}+y^{2}}$，则正弦函数$\sin\alpha=\frac{y}{r}$，余弦函数$\cos\alpha=\frac{x}{r}$，正切函数$\tan\alpha=\frac{y}{x}(x\neq0)$。通过对角的概念在不同象限的推广，我们可以得到任意角三角函数值的情况。例如，当角$\alpha$在第一象限时，$x\gt0,y\gt0$，$\sin\alpha\gt0,\cos\alpha\gt0,\tan\alpha\gt0$；而在第二象限，$x\lt0,y\gt0$，$\sin\alpha\gt0,\cos\alpha\lt0,\tan\alpha\lt0$，以此类推。理解基本三角函数的定义是学习各类三角函数公式的前提，它为我们构建起三角函数与直角坐标系中坐标的联系。

三、同角三角函数的基本关系

1. 平方关系：$\sin^{2}\alpha+\cos^{2}\alpha = 1$。这个公式犹如一个神奇的等式，它将正弦和余弦函数紧密地联系在一起。在这个等式中，无论$\alpha$取何值，只要是在三角函数的定义域内，等式始终成立。它在我们进行三角函数的化简、求值过程中发挥着重要作用。例如，已知$\sin\alpha=\frac{3}{5}$，且$\alpha$在第一象限，我们可以利用平方关系求出$\cos\alpha$的值：$\cos\alpha=\sqrt{1 - \sin^{2}\alpha}=\sqrt{1 - (\frac{3}{5})^{2}}=\frac{4}{5}$。
2. 商数关系：$\tan\alpha=\frac{\sin\alpha}{\cos\alpha}(\cos\alpha\neq0)$。从几何角度看，在单位圆中，正切函数表示终边上一点的纵坐标与横坐标的比值。当$\cos\alpha = 0$时，$\tan\alpha$无意义。这个关系式在处理正切函数与其他三角函数的转化以及进行三角函数的计算和变形时非常实用。比如，在化简$\frac{\sin\alpha}{\cos\alpha}+\cos\alpha$时，我们就可以将其转化为$\tan\alpha+\cos\alpha$，使式子更加简洁。
3. 倒数关系：$\sin\alpha\cdot\csc\alpha = 1$，$\cos\alpha\cdot\sec\alpha = 1$，$\tan\alpha\cdot\cot\alpha = 1$，其中$\csc\alpha$是余割函数，$\sec\alpha$是正割函数，$\cot\alpha$是余切函数。这些倒数关系在解决一些特定的三角函数问题时，可以帮助我们进行运算和化简。例如，在已知$\csc\alpha = 2$时，我们可以直接得出$\sin\alpha=\frac{1}{2}$。

四、诱导公式

诱导公式如同一位神奇的魔法师，它能够将任意角的三角函数转化为锐角三角函数，从而使我们在处理复杂角度问题时更加得心应手。

1. 终边相同的角的诱导公式：$\sin(\alpha + 2k\pi)=\sin\alpha$，$\cos(\alpha + 2k\pi)=\cos\alpha$，$\tan(\alpha + k\pi)=\tan\alpha$（$k\in Z$）。这意味着角的终边每旋转$2\pi$弧度（$360^{\circ}$），其三角函数值保持不变。例如，$\sin(45^{\circ}+360^{\circ})=\sin45^{\circ}=\frac{\sqrt{2}}{2}$，这就如同一个旋转的齿轮，每转一圈就会回到初始状态，其对应的三角函数值也随之不变。
2. 关于$k\cdot\frac{\pi}{2}\pm\alpha$的诱导公式：这些公式涵盖了多种角度变换的情况。如$\sin(-\alpha)=-\sin\alpha$，体现了三角函数的奇偶性；$\sin(\pi - \alpha)=\sin\alpha$，$\cos(\pi - \alpha)=-\cos\alpha$等。通过这些公式，我们可以将不同象限的角的三角函数统一转化为已知角的三角函数。比如，求$\sin150^{\circ}$的值，根据诱导公式$\sin150^{\circ}=\sin(180^{\circ}- 30^{\circ})=\sin30^{\circ}=\frac{1}{2}$。

五、两角和与差的三角函数公式

1. 两角和与差的正弦公式：$\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta$。这个公式犹如一把开启三角函数复杂运算之门的钥匙。例如，计算$\sin(15^{\circ})$，我们可以将$15^{\circ}$表示为$45^{\circ}- 30^{\circ}$，然后利用两角差的正弦公式：$\sin(45^{\circ}- 30^{\circ})=\sin45^{\circ}\cos30^{\circ}-\cos45^{\circ}\sin30^{\circ}=\frac{\sqrt{2}}{2}\times\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}\times\frac{1}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$。
2. 两角和与差的余弦公式：$\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta$。它在解决诸如求$\cos(75^{\circ})$之类的问题时非常有用，$75^{\circ}=45^{\circ}+ 30^{\circ}$，则$\cos(45^{\circ}+ 30^{\circ})=\cos45^{\circ}\cos30^{\circ}-\sin45^{\circ}\sin30^{\circ}=\frac{\sqrt{6}-\sqrt{2}}{4}$。
3. 两角和与差的正切公式：$\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}$。在已知$\tan\alpha$和$\tan\beta$的值时，我们可以利用这个公式快速求出$\tan(\alpha\pm\beta)$的值。

六、二倍角、半角公式

1. 二倍角公式：$\sin2\alpha = 2\sin\alpha\cos\alpha$，$\cos2\alpha=\cos^{2}\alpha-\sin^{2}\alpha = 2\cos^{2}\alpha - 1 = 1 - 2\sin^{2}\alpha$，$\tan2\alpha=\frac{2\tan\alpha}{1 - \tan^{2}\alpha}$。这些公式在三角函数的化简、求值和证明中具有重要作用。例如，在化简$\sin2x+\cos2x$时，我们可以根据选用不同形式的二倍角公式，或者将其变形为$\sqrt{2}\sin(2x + 45^{\circ})$，从而便于进一步分析其性质。
2. 半角公式：$\sin\frac{\alpha}{2}=\pm\sqrt{\frac{1 - \cos\alpha}{2}}$，$\cos\frac{\alpha}{2}=\pm\sqrt{\frac{1+\cos\alpha}{2}}$，$\tan\frac{\alpha}{2}=\frac{1 - \cos\alpha}{\sin\alpha}=\frac{\sin\alpha}{1+\cos\alpha}$。在已知角的值时，可以利用半角公式求出其一半角的三角函数值，但需要注意根据角的象限来确定正负号。

三角函数公式众多而又相互关联，它们构成了一个完整的体系。只有将各个公式理解透彻、灵活运用，才能在数学的海洋中畅游，在解决实际问题的过程中充分发挥三角函数的强大威力。无论是应对考试中的各类数学问题，还是在科学研究和技术应用中遇到与角度、周期性变化相关的情况，熟练掌握三角函数公式都将为我们提供有力的支持，帮助我们更为高效地进行分析和处理。