三角函数公式：解析与运用

在数学的浩瀚星海中，三角函数犹如璀璨星辰，照亮了众多科学与工程领域的征途。它们不仅承载着数千年数学文明的精髓，更是连接几何与代数，现实与理论的桥梁。本文将深入浅出地探讨三角函数的基本公式及其应用，带领读者领略这一数学分支的独特魅力。

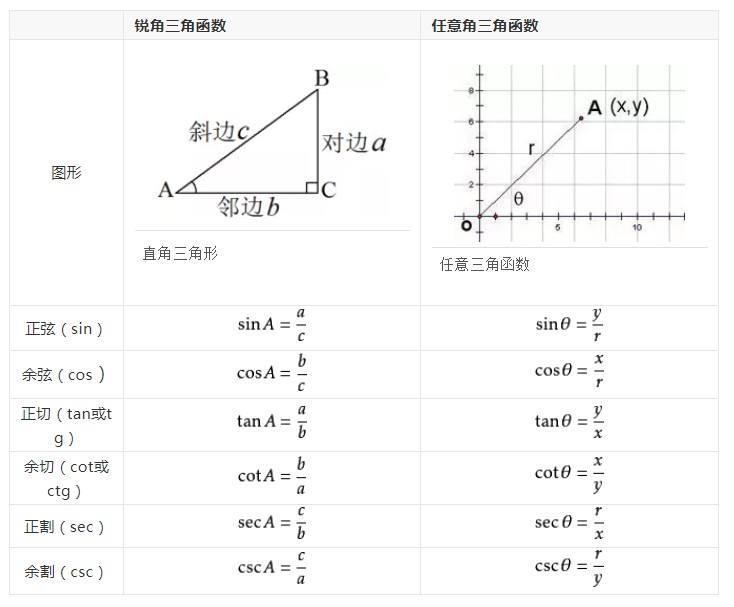
基本三角函数

三角函数主要包括正弦（sin）、余弦（cos）、正切（tan）、余切（cot）、正割（sec）和余割（csc）六大函数。它们分别定义在直角三角形的边长比例上，例如，对于一个任意角θ，正弦函数sinθ表示该角对边与斜边之比，余弦函数cosθ则是邻边与斜边之比。这些基础定义，是理解和运用更复杂三角函数公式的基石。

和角与差角公式

三角函数的和角与差角公式是其核心工具之一，它们使得我们可以将两个角的函数值转化为单一角度的函数运算。例如，sin(A ± B) = sinAcosB ± cosAsinB，这类公式在解决三角函数的和、差问题时极为有效，尤其是在傅里叶分析、波动方程等高级数学领域，展现了其强大的应用潜力。

二倍角与半角公式

二倍角公式，如sin2θ = 2sinθcosθ，允许我们将一个角度的两倍函数转换为该角度的基本函数组合，极大简化了公式表达和计算过程。而半角公式，如cos²(θ/2) = (1 + cosθ)/2，则提供了从大角度向小角度转换的方法，这对于需要精确解或数值逼近的问题至关重要。

乘积到和与和到乘积的转换

三角函数的另一个重要特性是其乘积与和之间的转换能力。例如，通过使用积化和差公式，可以将sinAsinB或cosAcosB等乘积形式转化为sin(A ± B)或cos(A ± B)的和差形式，反之亦然。这些转换技术在积分计算、解微分方程等方面有着广泛应用，是简化计算、求解复杂问题的关键。

应用实例

三角函数公式不仅在纯数学领域内发挥着不可或缺的作用，其影响力还延伸至物理学、工程学、天文学乃至音乐理论等多个领域。例如，在物理学中，简谐运动的描述离不开正弦和余弦函数；在建筑学中，三角函数帮助设计师精确计算结构的角度和距离；在音乐理论中，声波的波形分析也依赖于三角函数的理解和应用。

总之，三角函数公式是数学语言中不可或缺的一部分，它们以精确而优雅的方式描述了自然界中的周期现象，无论是在理论研究还是实践应用中，都展现出无穷的价值与魅力。深入学习并掌握这些公式，不仅能提升我们的数学素养，更能为解决实际问题提供强有力的工具。